诊断准确性试验设计
单组设计 - 基于ROC的曲线下面积的样本量估计
示例1:
参考文献中的示例:
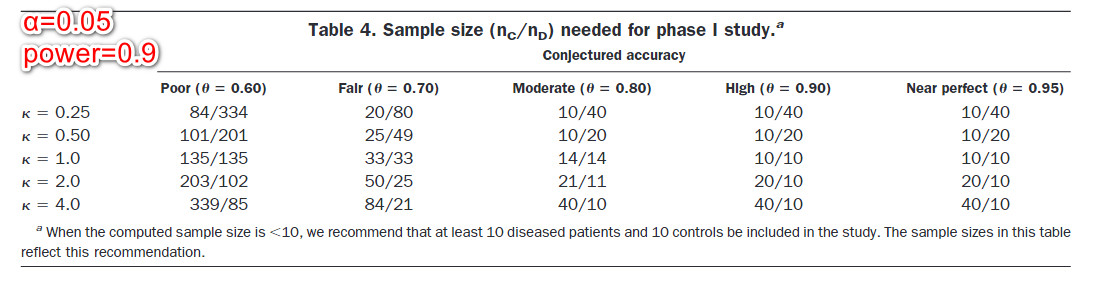
For a balanced design (equal numbers of patients with and without disease), if the accuracy of the diagnostic test is expected to be fair (e.g., 0.70), then 33 control patients and 33 diseased patients (total of 66 patients) are needed.
$\alpha$=0.05,$power$=0.9
$\theta$=0.7,$k$=1
$\alpha$=0.05,$power$=0.9
$\theta$=0.7,$k$=1

参数说明:
- $\alpha$,一类错误,检验水准,结果为假阳性的概率。α越小,即检验水准要求越高,正态分布对应的Z值越大,样本量要求越大。
- AUC一般总是大于等于0.5,其假设检验为单侧检验。 $$单侧检验的无效假设:\theta≤0.5$$ $$单侧检验的备择假设:\theta>0.5$$
- $1-\beta$,检验效应,等于1-II类错误($\beta$),表示当存在差异时,假设检验能得到阳性结果的概率。一般要求检验效能在0.8以上,否则会出现非真实的阴性结果。
- $\theta$,预估计的ROC曲线下面积(AUC)的值,可通过文献和预实验估计。
- $k$,最终纳入人群中未患病人数和患病人数之比。
- 页面计算码:样本量计算花费开发者(黄桥)大量时间进行整理和网页开发,请关注作者个人公众号,发送“计算码”获取最新码。
计算公式(需输入计算码):
1、估计所需患病人数
单侧检验:
$$n_{disease}=\frac{[Z_{1-\alpha}*\sqrt{0.0792*(1+1/k)}+Z_{1-\beta}*\sqrt{V(\hat{\theta})}]^2}{(\theta-0.5)^2}$$其中, $$V(\hat{\theta})=(0.0099*e^{-A^2/2})*([5*A^2+8]+[A^2+8]/k)$$ $$A=\Phi^{-1}(\theta)*1.414$$